Airline Flight Agenda Scheduling Problem using Dijkstra’s Algorithm

For our Algorithm and Complexity Course here at Kathmandu University, I was given this mini project to work on Airline Flight Agenda Scheduling problem using shortest path algorithm.

Here in this blog I am going to explain the implementation of Dijkstra’s Algorithm for creating a flight scheduling algorithm and solving the problem below, along with the Python code.

And, if you are in a hurry, here is the GitHub repo link of the project.

Problem Statement – Airline Flight Scheduling Algorithm

A travel agent requests software for making an agenda of flights for clients. The agent has access to a data base with all airports and flights. Besides the flight number, origin airport and destination, the flights have departure and arrival time. Specifically the agent wants to determine the earliest arrival time for the destination given an origin airport and start time.

A few Google search and I found out, the problem was similar to the airline flight agenda scheduling problem example given here in this page.

Problem Overview – Shortest Path Algorithm

This is the shortest path algorithm problem as we need to calculate the earliest arrival time, with a given start time. So, we can take the problem as a di graph where all the airports are nodes and the flights are the di edges with weight of time interval i.e. the time difference between arrival time of destination airport and departure time of source airport.

Here we need to take care that while going from origin airport to destination airport, and while taking flights from one airport to another, we can take only those flights which can be caught.

So, time plays an important role in this problem as we can take only the flights whose departure time from the airport is later than our arrival time at the airport.

So, to solve this we use Dijkstra’s Algorithm with a little modification.

Dijkstra’s Algorithm:

Dijkstra’s Algorithm is a shortest path algorithm used to calculate the shortest path between nodes in a graph. This algorithm was created and published by computer scientist Dr. Edsger W. Dijkstra.

The algorithm exists in many variants. Dijkstra’s original algorithm was to find the shortest path between two given nodes, but a more common variant fixes a single node as the “source” node and finds shortest paths from the source to all other nodes in the graph, producing a shortest-path tree.

Dijkstra’s Algorithm Priority Queue

In Dijkstra’s algorithm, we start from a source node and initialize its distance by zero. Next, we push the source node to a priority queue with a cost equal to zero. After that, we perform multiple steps.

In each step, we extract the node with the lowest cost, update its neighbors’ distances, and push them to the priority queue if needed.

Each of the neighboring nodes is inserted with its respective new cost, which is equal to the cost of the extracted node plus the edge we just passed through. We continue to visit all nodes until there are no more nodes to extract from the priority queue. Then, we return the calculated distances.

Our Algorithm Explained – Dijkstra Algorithm Example Explained

The algorithm for this problem is the slight modification of Dijkstra’s Algorithm. Here we have the database about airports and the flights. There is information about flight number, origin airport and destination, the flights have departure and arrival time. So, given origin and destination airports and start time we need to make our data structure properly to keep the data and find the shortest arrival time.

Here the di graph is used where the airports are the vertices and flights are di-edges with weights: departure time and arrival time. The distance should be the function of earliest arrival times at airports. Then based upon those earliest arrival time, we use a minimum priority queue for airports.

For the initial origin airport let the earliest arrival time be start time and for others it will be infinity in the beginning. Now, until the queue is not empty, adjacent loop is to be formed where we can only select the flights which can be caught, and we also want the flight with minimum arrival time.

So, for that we create another priority queue of flights where its departure time should be later than arrival time of another flight at the airport. And we also use another variable time, which is used to update the flight priority queue.

And finally, we perform relaxation, where if the above time is less than the earliest arrival time at adjacent airport, then we change the earliest arrival time of the airport to be the time and update in the airport queue accordingly.

Lets Code – Dijkstra Algorithm Python Code

I use VS Code and its my favorite code editor. Which one is yours?

Here we create a new file flight.py.

Flight.py

import queue

class Flight:
    def __init__(self, name, origin, dest, arrivalT, departT):
        self.name = name
        self.origin = origin
        self.dest = dest
        self.arrivalT = arrivalT
        self.departT = departT
        self.weight = departT - arrivalT

    def __str__(self):
        return str(self.origin) + " - " + str(self.dest)

    def __repr__(self):
        return self.__str__()

    def __lt__(self, other):
        return self.arrivalT < other.arrivalT


class Graph:
    def __init__(self, vertices):
        self.vertices = vertices

class Schedule:
    def __init__(self, vertex, time):
        self.vertex = vertex
        self.time = time

    def __hash__(self):
        return hash(str(self.vertex) + ":" + str(self.time))

    def __lt__(self, other):
        return self.time < other.time

    def __str__(self):
        return "{" + str(self.vertex) + ":" + str(self.time) + "}"

    def __repr__(self):
        return self.__str__()

    def __eq__(self, other):
        if isinstance(other, Schedule):
            return (self.vertex == other.vertex) and (self.time == other.time)
        return False

class Vertex:

    def __init__(self, name, adjacentVertices):
        self.name = name
        self.adjacentVertices = adjacentVertices

    def __str__(self):
        return self.name

    def __repr__(self):
        return self.__str__()

    def __eq__(self, other):
        if isinstance(other, Vertex):
            return self.adjacentVertices == other.adjacentVertices
        return False

    def __hash__(self):
        return hash(str(self.name))


def FlightAgency(F, G, s, d, startT):

    T = {}
    T[s] = startT

    # for all vertex, v != s do T[v] ← infinity
    for vertex in G.vertices:
        if(vertex is not s):
            T[vertex] = float("inf")

    # Priority Queue, q, of vertices keyed by T
    q = queue.PriorityQueue()
    for vertex in G.vertices:
        q.put(Schedule(vertex, T[vertex]))

    while not q.empty():
        v = q.get()

        for adjacentVertex in v.vertex.adjacentVertices:
            if Schedule(adjacentVertex, T[adjacentVertex]) in q.queue:

                p = queue.PriorityQueue()
                for flight in F:
                    if(flight.origin == v.vertex and 
                    flight.dest == adjacentVertex):
                        if(flight.departT >= T[v.vertex]):
                            p.put(flight)

                t = float("inf")

                if not p.empty():
                    t = p.queue[0].arrivalT

                # relaxation
                if t < T[adjacentVertex]:
                    T[adjacentVertex] = t
                    q.put(Schedule(adjacentVertex, t))

            else:
                break
    
    earliestTime = T[d]
    
    return earliestTime

Breaking Down the Code:

Here we create some classes. First there is the class Graph, which will have vertices. Then there is Vertex class for the airport which will have the airport details. Class flight will have the flight name, origin, destination, arrival time and departure time.

As we have mentioned earlier, the flight difference between the arrival and departure time will be the weights. For listing the flight schedules, we have created a Schedule class.

Then there is the main function FlightAgency(), which calculates the required earliest arrival time using the algorithm above.

As for the main file here, we create a new file named main.py.

main.py

from flight import Flight, Vertex, Graph, FlightAgency

# The airports as vertices
airportE = Vertex("E", [])
airportD = Vertex("D", [airportE])
airportB = Vertex("B", [airportD, airportE])
airportC = Vertex("C", [airportB])
airportA = Vertex("A", [airportC, airportB])

def run():

    # List the flights for airports
    flights = [
        Flight('FN-101', airportA, airportB,  6, 2),
        Flight('FN-102', airportA, airportC,  8, 2),
        Flight('FN-103', airportB, airportD,  13, 12),
        Flight('FN-104', airportB, airportE,  17, 11),
        Flight('FN-105', airportC, airportB,  10, 9),
        Flight('FN-106', airportC, airportD,  10, 6,),
        Flight('FN-107', airportD, airportE,  14, 13),
    ]

    # Graph with airports as vertices
    graph = Graph([airportA, airportB, airportC, airportD, airportE])

    # Origin Airport be airportA and destination be airportE
    startVertex = airportA
    endVertex = airportE
    # Start time be 2 (Time in 24 hour format)
    startT = 2

    earliestArrivalTime = FlightAgency(flights, graph, startVertex, endVertex, startT)
    if (earliestArrivalTime != float("inf")):
        print(f'The earliest arrival time for the airport {endVertex} from airport {startVertex} is {earliestArrivalTime}:00.')
    else:
        print(f'No flight from airport {startVertex} to airport {endVertex} after {startT}:00.')

if __name__ == '__main__':
    run()

So, for our main program we made following setup:

• Airport A, B, C, D, E as the vertices of the Graph G.
• The list of 7 flights:
  • FN-101: From airport A to B with departure time 02:00 and arrival time 06:00
  • FN-102: From airport A to C with departure time 02:00 and arrival time 08:00
  • FN-103: From airport B to D with departure time 12:00 and arrival time 13:00
  • FN-104: From airport B to E with departure time 11:00 and arrival time 17:00
  • FN-105: From airport C to B with departure time 09:00 and arrival time 10:00
  • FN-106: From airport C to D with departure time 06:00 and arrival time 10:00
  • FN-107: From airport D to E with departure time 13:00 and arrival time 14:00

• The flights are the edges.
• Airport A as the origin airport.
• Airport E as the destination airport.
• 02:00 as the start time.
• Finally, we call the FlightAgency function.

We will get the result that,

So, starting at 02:00 from airport A the shortest path to reach airport E, the earliest arrival time is 14:00.

Unit Test – Dijkstra Test Cases

Here is a test case. Unittest library is used for test case. We use the function like test_flightagency to test the algorithms over test cases. For test case, we create a very simple graph and check for different cases like going to adjacent and non-adjacent airports, try to go to airport with flight missed, going to airport with no available flights, etc.

testFlight.py

import unittest
from flight import Flight, Vertex, Graph, FlightAgency

class TestFlight(unittest.TestCase):

    def setUp(self):
        self.airportE = Vertex("E", [])
        self.airportD = Vertex("D", [self.airportE])
        self.airportB = Vertex("B", [self.airportD])
        self.airportC = Vertex("C", [self.airportB])
        self.airportA = Vertex("A", [self.airportB, self.airportC, self.airportE])

        self.flights = [
            Flight('1', self.airportA, self.airportB,  2, 1),
            Flight('2', self.airportA, self.airportC,  4, 3),
            Flight('3', self.airportA, self.airportE,  12, 1),
            Flight('4', self.airportB, self.airportD,  6, 4),
            Flight('5', self.airportC, self.airportB,  5, 3),
            Flight('6', self.airportD, self.airportE,  8, 6),
        ]

        self.graph = Graph([self.airportA, self.airportB, self.airportC, self.airportD, self.airportE])

    def test_flightagency(self):
        # From A to B
        self.assertEqual( FlightAgency(self.flights, self.graph, self.airportA, self.airportB, 1), 2 )
        # From A to B after flight missed
        self.assertEqual( FlightAgency(self.flights, self.graph, self.airportA, self.airportB, 5), float('inf') )
        # From B to A
        self.assertEqual( FlightAgency(self.flights, self.graph, self.airportB, self.airportA, 1), float('inf') )

        # From A to C
        self.assertEqual( FlightAgency(self.flights, self.graph, self.airportA, self.airportC, 1), 4 )

        # To E
        self.assertEqual( FlightAgency(self.flights, self.graph, self.airportA, self.airportE, 1), 8 )
        self.assertEqual( FlightAgency(self.flights, self.graph, self.airportB, self.airportE, 1), 8 )

if __name__ == "__main__":
    unittest.main()

Analysis – Dijkstra Algorithm Example

Based upon the setup as in the main file, we would have got a graph like below:

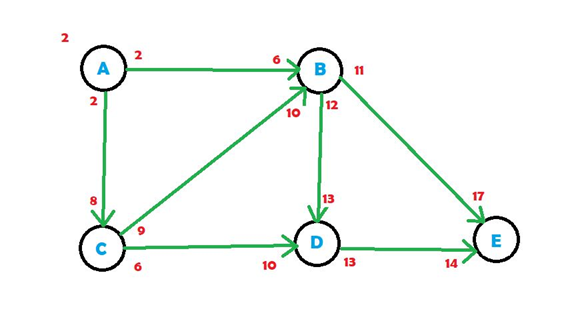
Easiest way for JavaScript Network Graph Visualization

In above graph, there is a flight that leaves from airport A at 2 and reaches C at 8 and another flight leaves airport A at 2 and reach airport B at 6 and so on.

From airport A, we can go to airport B and C. The best possible arrival time for airport B and C would be 6 and 8 respectively.

The flight from C to D departs at 6. So, starting at time 2 and reaching airport C at 8, there is no way we can catch that flight. So, from C, now we can only go to B. We can reach airport B either from A or from C, but the earliest arrival time would be from airport A at 6.

Similarly, from B we can go to D or E and so on. So, finally using the algorithm the best possible shortest pathway we can reach airport E from airport A would be via route A – B – D – E.

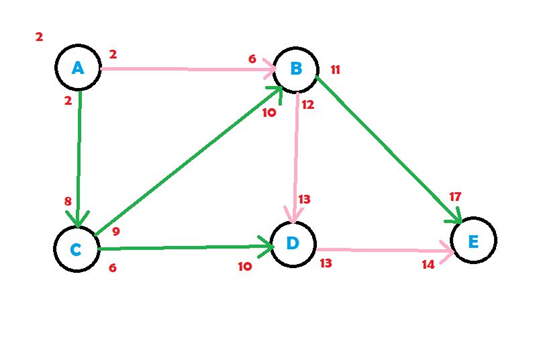
Easiest way for JavaScript Network Graph Visualization

And, using those flights, we would reach airport E at 14, which is the answer given by our program.

In this way we have implemented the Dijkstra’s Algorithm for airline flight agenda scheduling problem .

Due to the device width issue, for some devices the code lines above might have been altered and indentation might have been affected.

In such a case, the code is available in my GitHub.

If this was helpful, how about buying me a coffee ?